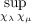On weak restricted estimates and endpoint problems for convolutions with oscillating kernels. I

Wolfgang B. Jurkat and Gary Sampson

Vol. 96 (1981), No. 2, 405–418

DOI: 10.2140/pjm.1981.96.405

Abstract

Throughout we consider K(t) = e^i|t|a ∕|t|^b, a > 0, a≠1, b < 1 and t ∈ R. Here we consider for fixed λ,μ > 0 the function B(λ,μ;K) = B(λ,μ) = ∫ χ_λ(x)K ∗χ_μ(x)dx where the sup is taken over all “characteristic” functions χ_λ, χ_μ with complex signs (i.e., χ_μ is a measurable function for which |χ_μ| = 1 on E, |χ_μ| = 0 off E and |E|≦ μ(μ > 0)). We estimate B(λ,μ;K) within constant factors from above and below. This settles the endpoint problems for these kernels, at least in the weak restricted sense.

Mathematical Subject Classification 2000

Primary: 47G05, 47G05

Secondary: 44A35

Milestones

Received: 16 February 1979

Revised: 15 December 1980

Published: 1 October 1981