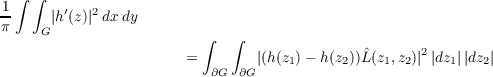A characterization of the adjoint L-kernel of Szegő type

Saburou Saitoh

Vol. 96 (1981), No. 2, 489–493

DOI: 10.2140/pjm.1981.96.489

Abstract

Let G be a bounded regular region in the complex plane and L(z,u) the adjoint L-kernel of Szegő kernel function K(z,ū) on G. Then, for any analytic function h(z) on G with a finite Dirichlet integral, it is shown that the equation

holds. Furthermore, for any fixed nonconstant h(z), we show that the function L(z₁,z₂) on G × G is characterized by that equation in some class.

Mathematical Subject Classification 2000

Primary: 30C40

Secondary: 30F99

Milestones

Received: 3 November 1980

Published: 1 October 1981