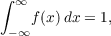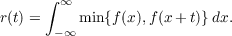|

|

|
|
Sample functions of
Pólya processes
Takayuki Kawada |
|
Vol. 97 (1981), No. 1, 125–135
|
Abstract |
||
|
For a nonnegative measurable function f satisfying
define
Berman proved, extending so-called “Polya characteristic function”, that the r is the characteristic function of an absolutely continuous distribution. The positive-definiteness of the r corresponds to a stationary Gaussian process, which is called Polya-Covariance process or simply Polya process. In this paper, some analytic properties of its sample functions are studied: (1) continuity, (2) differentiability, (3) quadratic variation, and (4) upper and lower class. |
Mathematical Subject Classification 2000
Primary: 60G15
Secondary: 60G17
|
Milestones
Received: 29 July 1980
Published: 1 November 1981
|
Authors |
| Takayuki Kawada | |
 |