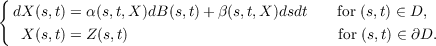Existence of strong solutions for stochastic differential equations in the plane

James Juei-Chin Yeh

Vol. 97 (1981), No. 1, 217–247

DOI: 10.2140/pjm.1981.97.217

Abstract

Let B be the 2-parameter Brownian motion on D = [0,∞] × [0,∞) and Z be a 2-parameter stochastic process defined on the boundary ∂D of D. Consider the non-Markovian stochastic differential system in 2-parameter

Under the assumption that the coefficients α and β satisfy a Lipschitz condition and a growth condition and the assumption that Z has continuous sample functions and locally bounded second moment on ∂D, it is shown in this paper that the differential system has a strong solution. Pathwise uniqueness of solution is established under the assumption of the Lipschitz condition.

Mathematical Subject Classification 2000

Primary: 60H10

Milestones

Received: 2 September 1980

Published: 1 November 1981