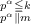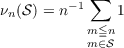An analogue of Kolmogorov’s inequality for a class of additive arithmetic functions

Joseph Eugene Collison

Vol. 97 (1981), No. 2, 319–325

DOI: 10.2140/pjm.1981.97.319

Abstract

Let f be a complex valued additive number theoretic function (i.e., f(mn) = f(m) + f(n) if m and n are relatively prime). This paper shows that ∑ D²(p^α)p^−α = O(D²(n)) or ∑ |f(p^α)|p^−α = O(D(n)) (where the summations are over those p^α ≦ n, p^α being a prime raised to a power) is sufficient to guarantee that the following analogue of Kolmogorov’s inequality holds:

where, if p^α∥m denotes the fact that p^α divides m but p^α+1 does not (i.e., p^α exactly divides m), then

A(n)	= ∑ pα≦nf(pα)p−α,
D2(n)	= ∑ pα≦n|f(pα)|2p−α,
fk(m)	= ∑ f(pα),

and

for any set 𝒮.

Mathematical Subject Classification

Primary: 10H25, 10H25

Secondary: 10K20

Milestones

Received: 22 July 1980

Revised: 24 October 1980

Published: 1 December 1981