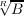Second note on Artin’s solution of Hilbert’s 17th problem. Order spaces

D. W. Dubois

Vol. 97 (1981), No. 2, 357–371

DOI: 10.2140/pjm.1981.97.357

Abstract

We consider real varieties in Kⁿ∕k, where K∕k is maximally ordered and k is dense in K. Our principal results are:

Theorem 1. Assume V is irreducible. A. The closure of the set of all simple points equals the set of all central points — z ∈ V is central if some order of k(V )∕k contains every function which is positive at z. B. If f + r is totally positive in k(V )∕k for every positive r in k, then f itself is totally positive.

Theorem 2. For a semi-algebraic set S in Kⁿ defined by polynomial relations b_j(x) = 0, g_i(x) > 0 (1 ≦ i,j ≦ m), define B = (b₁,⋯,b_m), G = {g₁,⋯,g_m}. Then every irreducible component of V _k(B) contains central points on S if and only if (∗) for 0 < p_i ∈ k, g_ij ∈ G, a_i ∈ k[X], ∑ _ip_iΠ_jg_ij a_i² ∈ implies every a_i ∈.

Mathematical Subject Classification 2000

Primary: 12D15

Secondary: 12J15, 14G30

Milestones

Received: 25 June 1980

Published: 1 December 1981