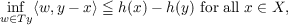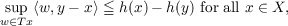A minimax inequality and its applications to variational inequalities

Chi-Lin Yen

Vol. 97 (1981), No. 2, 477–481

DOI: 10.2140/pjm.1981.97.477

Abstract

In this paper we get a slight generalization of a Ky Fan’s result which concerns with a minimax inequality. We shall use this result to give a direct proof for the existence of solutions of the following two variational inequalities:

(1)

and

(2)

where T ⊂ E ×E′ is monotone, E is a reflexive Banach space with its dual E′, X is a closed convex bounded subset of E, and h is a lower semicontinuous convex function from X into R.

Mathematical Subject Classification 2000

Primary: 49A29, 49A29

Secondary: 47H05

Milestones

Received: 20 June 1980

Revised: 27 October 1980

Published: 1 December 1981