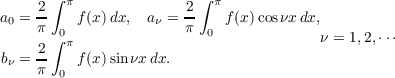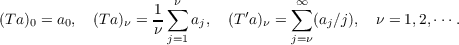On the transformation of Fourier coefficients of certain classes of functions

Suppose f(x) ∈ L¹(0,π) and let a = {a_ν} (b = {b_ν}) denote the Fourier cosine (sine) coefficients of f extended to (−π,π) as an even (odd) function, that is

∫ ∫ 2- π 2- π a0 = π 0 f(x)dx, aν = π 0 f(x)cosνx dx, 2∫ π ν = 1,2,⋅⋅⋅ bν = π- f(x)sinνx dx. 0

The sequence transformations T and T′ are defined by

ν ∞ (T a) = a , (T a) = 1-∑ a , (T ′a) = ∑ (a ∕j), ν = 1,2,⋅⋅⋅ . 0 0 ν ν j=1 j ν j=ν j

The purpose of this note is to characterize those rearrangement invariant function spaces L^σ(0,π) which are left invariant by the operators T and T′ acting on Fourier coefficients of functions in these spaces. Our results include and improve some results of Hardy, Bellman and Alshynbaeva.

Mathematical Subject Classification 2000

Primary: 42A16

Secondary: 46E30

Milestones

Received: 21 May 1980

Published: 1 June 1982

Authors

Kenneth F. Andersen

Vol. 100, No. 2, 1982

Kenneth F. Andersen

Abstract

Mathematical Subject Classification 2000

Milestones

Authors