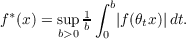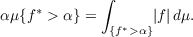Maximal functions for a semiflow in an infinite measure space

Ryōtarō Satō

Vol. 100 (1982), No. 2, 437–443

DOI: 10.2140/pjm.1982.100.437

Abstract

Let (X,ℱ,μ) be a σ-finite measure space and Γ = (𝜃_t : t ≧ 0) a measurable semiflow of measure preserving transformations on (X,ℱ,μ). The maximal function f^∗ of a function f ∈ L₁(μ) + L_∞(μ) is defined by

The purpose of this paper is to prove that if μ(X) = ∞ and the semiflow Γ is conservative and ergodic then for every constant α > 0

Mathematical Subject Classification 2000

Primary: 28D10

Milestones

Received: 20 August 1980

Published: 1 June 1982