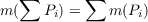Gleason’s theorem for type I von Neumann algebras

Jürgen Tischer

Vol. 100 (1982), No. 2, 473–488

DOI: 10.2140/pjm.1982.100.473

Abstract

For a von Neumann algebra A a G-measure m on A is defined as a map from the projections of A to the positive reals which satisfies the equation

for every family (P_i) of pairwise orthogonal projections. We prove the following generalization of Gleason’s theorem: If m is a G-measure on a type I von Neumann algebra A not containing a type I₂ direct summand, then there exists an extension of m to a positive normal linear for on A.

Mathematical Subject Classification

Primary: 46L50, 46L50

Secondary: 81B10

Milestones

Received: 12 June 1980

Revised: 8 October 1980

Published: 1 June 1982