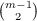|
Let m ≧ 1, and let H be the
multiplicative free abelian group of rank m, with integral group ring ZH and
augmentation ideal IH. Suppose 0 → B → A → IH → 0 is a short exact sequence of
ZH-modules, and the module A is finitely generated. Then A and B are both finitely
presented, and for any k ∈ Z the determinantal ideals Ek(A) and Ek−1(B) satisfy the
inclusions
where 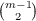 is the binomial coefficient (and in particular is the binomial coefficient (and in particular 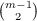 = 0 if m ≦ 2), and
(IH)0 = ZH. In particular, if m = 1 then Ek(A) = Ek−1(B) for any k ∈ Z. A
consequence of these inclusions is the fact that the greatest common divisors
Δk(A) = Δk−1(B) for any k ∈ Z. = 0 if m ≦ 2), and
(IH)0 = ZH. In particular, if m = 1 then Ek(A) = Ek−1(B) for any k ∈ Z. A
consequence of these inclusions is the fact that the greatest common divisors
Δk(A) = Δk−1(B) for any k ∈ Z.
|



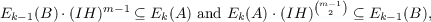
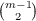 is the binomial coefficient (and in particular
is the binomial coefficient (and in particular