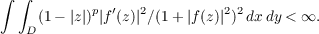Nonnormal Blaschke quotients

Shinji Yamashita

Vol. 101 (1982), No. 1, 247–254

DOI: 10.2140/pjm.1982.101.247

Abstract

A quotient B₁∕B₂ of two infinite Blaschke products B₁ and B₂ with no common zero is called a Blaschke quotient. The existence of a Blaschke quotient which is not normal in the open unit disk D, is well known. We shall show among other things, that, for each p, 0 < p < ∞, there exists a nonnormal Blaschke quotient f such that

This might be of interest because, if g is meromorphic in D and if ∫ ∫ _D|g′(z)|²∕(1 + |g(z)|²)² dxdy < ∞, then g is normal in D.

Mathematical Subject Classification 2000

Primary: 30D45

Secondary: 30D50

Milestones

Received: 6 April 1979

Published: 1 July 1982