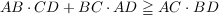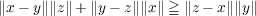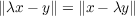Ptolemy’s inequality, chordal metric, multiplicative metric

M. S. Klamkin and A. Meir

Vol. 101 (1982), No. 2, 389–392

DOI: 10.2140/pjm.1982.101.389

Abstract

Ptolemy’s inequality in R² states: If A, B, C, D are vertices of a quadrilateral, then

with equality only ABCD is a convex cyclic quadrilateral. A real normed linear vector space is called ptolemaic if

for all x, y and z in the space and it is called symmetric if

for all unit vectors x, y and real λ. The equivalence of these two properties of a normed linear space is established and related results concerning distance functions in such spaces are proven.

Mathematical Subject Classification 2000

Primary: 51K05

Secondary: 46B99

Milestones

Received: 2 May 1980

Published: 1 August 1982