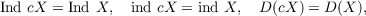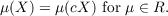|
|||||

|

|
|

|

|
|
On compactifications
of metric spaces with transfinite dimensions
Leonid A. Luxemburg |
|
Vol. 101 (1982), No. 2, 399–450
|
Abstract |
||
|
In this paper we prove that every separable metric space X with transfinite dimension IndX has metric compactification cX such that
where ind X (Ind X) denotes small (large) inductive transfinite dimension, and D(X) denotes the transfinite D-dimension. More generally, let T be a set of invariants (ind,Ind,D). We consider the following problem: Let R ⊆ T and X be a metric space. Does there exist a bicompactum (complete space) cX ⊃ X such that
When it is not so, we give counterexamples. We give also necessary and sufficient conditions of the existence of transfinite dimensions of separable metric space in terms of compactifications. |
Mathematical Subject Classification 2000
Primary: 54F45
|
Milestones
Received: 5 March 1979
Revised: 12 February 1981
Published: 1 August 1982
|
Authors |
| Leonid A. Luxemburg | |
 |