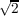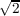|
The generalized Gauss map
of an immersed oriented surface M in R4 is the map which associates to each point
of M its oriented tangent plane in G2,4, the Grassmannian of oriented planes in
R4. The Grassmannian G2,4 is naturally identified with Q2, the complex
hyperquadric
The normalized Fubini-Study metric on P3(C) with holomorphic curvature 2
induces an invariant metric on Q2≅G2,4, which corresponds exactly to the
metric on the canonical representation of S2(1∕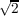 ) × S2(1∕ ) × S2(1∕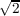 ) in R6 as
{X ∈ R6∣x12 + x22 + x32 = (1∕2),x42 + x52 + x62 = (1∕2)}. The product
representation above allows us to associate with any map g in Q2 two canonical
projections g1, g2. In the case where g is complex analytic map defined on
some Riemann surface S0, the projections g1, g2 are complex analytic
also. Detailed treatment can be found in the recent work of Hoffman and
Osserman. ) in R6 as
{X ∈ R6∣x12 + x22 + x32 = (1∕2),x42 + x52 + x62 = (1∕2)}. The product
representation above allows us to associate with any map g in Q2 two canonical
projections g1, g2. In the case where g is complex analytic map defined on
some Riemann surface S0, the projections g1, g2 are complex analytic
also. Detailed treatment can be found in the recent work of Hoffman and
Osserman.
|



![∑4 2 3
{[z1,z2,z3,z4]| zk = 0} in P (C ).
k=1](a020x.png)