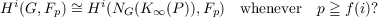An affirmative answer to Glauberman’s conjecture

Masahiko Miyamoto

Vol. 102 (1982), No. 1, 89–105

DOI: 10.2140/pjm.1982.102.89

Abstract

Let G be a finite group and P be a Sylow p-subgroup of G for a prime p. The following question is raised by G. Glauberman.

Question 16.8. Does there exist a function f from the positive integers i to the positive integers such that

Here K_∞ denotes the section conjugacy functor constructed by G. Glauberman and F_p denotes the finite field consisting of p elements and by forgetting its multiplicative structure, we consider it as a trivial G-module.

In relation to the above conjecture, he proved the case i = 1 and D. F. Holt has recently proved f(2) ≦ 11. The purpose of this paper is to provide an affirmative answer to the question.

Theorem C. If p ≧ 12 × 6^m−2 + 3, the H^m(G,F_p)≅H^m(N_G(K_∞(P)),F_p) for all integers m ≧ 2.

Mathematical Subject Classification 2000

Primary: 20J06

Milestones

Published: 1 September 1982