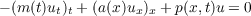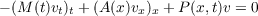Picone-type theorems for hyperbolic partial differential equations

Kurt Kreith

Vol. 102 (1982), No. 2, 385–395

DOI: 10.2140/pjm.1982.102.385

Abstract

Sturmian comparison theorems are established for hyperbolic partial differential equations of the form

and

when these equations are neither assumed to admit a separation of variables, nor to have equal principal parts. As such, the principal results constitute a generalization of the classical Sturm-Picone theorem.

Mathematical Subject Classification 2000

Primary: 35B05

Secondary: 35L10

Milestones

Received: 13 January 1981

Revised: 18 May 1981

Published: 1 October 1982