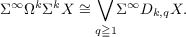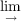|

|

|
|
The geometry of the
James-Hopf maps
Nicholas J. Kuhn |
|
Vol. 102 (1982), No. 2, 397–412
|
Abstract |
|
|
Snaith’s splitting of the suspension spectrum of the space ΩkΣkX, for X path connected, into the wedge of the suspension spectra of spaces denoted Dk,qX, has been of considerable interest to homotopy theorists in recent years. If Σ∞X denotes the suspension spectrum of a space X then this can be restated as
Projection onto the q-th wedge summand and adjunction yield James-Hopf maps
jq : ΩkΣkX → QDk,qX, where QY = In this paper I study various compatibility relations which hold among the jq as X is replaced by ΣnX. In particular, I show that, for k > n, the iterated evaluation map 𝜀n : ΣnΩkΣkX → Ωk−nΣkX is naturally compatible with the stable splittings of these two spaces. This is done by exhibiting maps δk,n : ΣnDk,qX → Dk−n,qΣnX making the following diagram of suspension spectra homotopy commute: 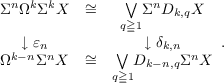 In certain cases, the maps δk,n are then identified as standard projection maps. Consequences are then discussed. |
Mathematical Subject Classification 2000
Primary: 55P35
Secondary: 55P47
|
Milestones
Received: 10 December 1980
Published: 1 October 1982
|
Authors |
| Nicholas J. Kuhn | |
| Department of Mathematics University of Virginia Kerchof Hall PO Box 400137 Charlottesville VA 22904-4137 United States |
|
| http://artsandsciences.virginia.edu/mathematics/people/faculty/njk4x.html | |
 |