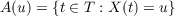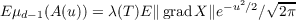|
If X(t1,t2,⋯,td) is a
sufficiently regular, centered, stationary Gaussian process, the (random) level set over
a measurable domain T ⊂ Rd
is a d − 1-dimensional manifold embedded in Rd. Our main result states that its
expected measure is given by
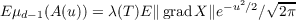 | (1) |
where μd−1(A) is the d − 1-dimensional volume of the hypersurface A, λ is the
Lebesgue measure on Rd and the variance of X is assumed to be one.
The expression (1) holds even for d = 1. In that case μ0(A) is a counting measure
that gives the number of points in A. (μ1 and μ2 give respectively length and
area.)
|