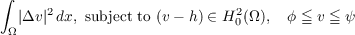|
|||||

|

|
|

|

|
|
The two-obstacle
problem for the biharmonic operator
Luis A. Caffarelli, Avner Friedman and Alessandro Torelli |
|
Vol. 103 (1982), No. 2, 325–335
|
Abstract |
|
|
In this work we consider a two-obstacle problem for the plate, namely, the problem of finding a minimizer u of
where Ω is a bounded domain in Rn; n = 2,3. We prove that u ∈ C1,1 and that, in general, u∉C2. |
Mathematical Subject Classification 2000
Primary: 35J85
Secondary: 49A29
|
Milestones
Received: 29 September 1980
Published: 1 December 1982
|
Authors |
| Luis A. Caffarelli | |
| Department of Mathematics University of Texas at Austin 1 University Station C1200 Austin TX 78712-0257 United States |
|
| http://www.ma.utexas.edu/users/caffarel/ | |
| Avner Friedman | |
| Alessandro Torelli | |
 |