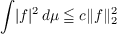Carleson measures for functions orthogonal to invariant subspaces

William S. Cohn

Vol. 103 (1982), No. 2, 347–364

DOI: 10.2140/pjm.1982.103.347

Abstract

Let D = {z : |z| < 1} be the unit disk. Suppose φ is an inner function with singular support K and let M^⊥ = H² ⊖φH² where H² is the usual class of functions holomorphic on D. If μ is a positive measure on D, the closed disk, which assigns zero mass to K, then call μ a Carleson measure for M^⊥ if for a c > 0,

for all f ∈ M^⊥. (Here and elsewhere, ∥f∥₂ denotes the H² norm of an H² function.) In this paper the Carleson measures for M^⊥ are characterized for all inner functions φ such that for some 𝜀, 0 < 𝜀 < 1, the set {z : |φ(z)| < 𝜀} is connected.

Mathematical Subject Classification 2000

Primary: 30D55

Secondary: 47B35

Milestones

Received: 9 September 1981

Published: 1 December 1982