|
|||||

|

|
|

|

|
|
Strong result for
real zeros of random polynomials
M. N. Mishra, N. N. Nayak and Swadeenananda Pattanayak |
|
Vol. 103 (1982), No. 2, 509–522
|
Abstract |
|
Let Nn be the number of real zeros of Σr=0narXrxr = 0 where Xr’s are independent random variables identically distributed belonging to the domain of attraction of normal law; a0,a1,a2⋯an are nonzero real numbers such that (kn∕tn) = o(log n) where kn = max0≦r≦n|ar| and tn = min0≦r≦n|ar|. Further we suppose that the coefficients have zero means and P{Xr≠0} > 0. Then there exists a positive integer n0 such that 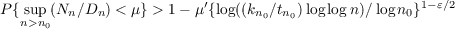 for n > n0 and 1 > 𝜀 > 0 where Dn = (log n∕log(kn∕tn)log log n)(1−𝜀)∕2. |
Mathematical Subject Classification 2000
Primary: 60G99
|
Milestones
Received: 19 August 1980
Revised: 16 September 1981
Published: 1 December 1982
|
Authors |
| M. N. Mishra | |
| N. N. Nayak | |
| Swadeenananda Pattanayak | |
 |
