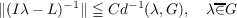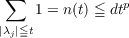Estimates of meromorphic functions and summability theorems

Andrei Shkalikov

Vol. 103 (1982), No. 2, 569–582

DOI: 10.2140/pjm.1982.103.569

Abstract

The main goal of this paper is to prove the following theorem.

Theorem 1. Let L be an unbounded operator in a Hilbert space H, having a discrete spectrum {λ_j}⊂ G = B_R ∪ P_q,h, where B_R = {λ : |λ|≦ R}, P_q,h = {λ : Re λ ≧ 0,|λ| > 1,|Im λ|≦ h(Re λ)^q,h > 0,−∞ < q < 1}, and for some γ < ∞, L⁻¹ ∈ σ_γ. Also let the estimate

hold outside the domain G′ = B_R ∪ P_q,2h, and for some a > 0, p > 0

provided t is sufficiently large.

Then L ∈ A(α,H) for any α > max0, p − (1 − q).

Besides, if the numbers a or h can be chosen arbitrarily small and p− (1 −q) > 0, then α = p − (1 − q) is admissible.

Mathematical Subject Classification 2000

Primary: 47A70

Secondary: 30D30

Milestones

Received: 14 April 1980

Published: 1 December 1982