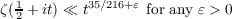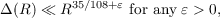On the order of ζ(1 2 + it) and Δ(R)

Grigori Abramovich Kolesnik

Vol. 98 (1982), No. 1, 107–122

DOI: 10.2140/pjm.1982.98.107

Abstract

In this paper we obtain new estimates of ζ(1∕2 + it), the value of the Riemann zeta-function on the critical line, and Δ(R), the remainder in the Dirichlet divisor problem.

The estimates are

and

which improve previously known best results.

Mathematical Subject Classification

Primary: 10H25, 10H25

Secondary: 10H05

Milestones

Received: 5 May 1976

Published: 1 January 1982