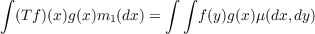Characterization and order properties of pseudo-integral operators

Ahmed Ramzy Sourour

Vol. 99 (1982), No. 1, 145–158

DOI: 10.2140/pjm.1982.99.145

Abstract

Let (X,𝒜,m₁) and (Y,ℬ,m₂) be separable σ-finite measure spaces. A linear transformation T from an order-ideal L of measurable functions on Y into the space of measurable functions on X is called a pseudo-integral operator if it is induced by a measure μ on X × Y via the equation

for sufficiently many functions g. Our main theorem states that T is a pseudo-integral operator if and only if Tf_n → 0 a.e. whenever 0 ≦ f_n ≦ f ∈ L and f_n → 0 a.e. We also study the order structure of the class of pseudo-integral operators showing that they form a band (order-closed ideal) in the space of order-bounded operators.

Mathematical Subject Classification 2000

Primary: 47B38

Milestones

Received: 3 March 1980

Revised: 30 July 1980

Published: 1 March 1982