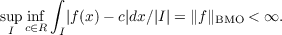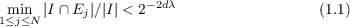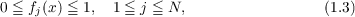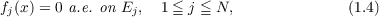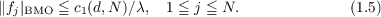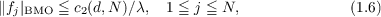The construction of certain BMO functions and the corona problem

In Euclidean space R^d, let I denote any cube with sides parallel to the axes and write |I| for the measure of I. A real valued locally integrable function f(x) on R^d has bounded mean oscillation, f ∈ BMO, if

∫ supinf |f(x)− c|dx∕|I| = ∥f∥ < ∞. I c∈R I BMO

Our result is the following.

Theorem 1. Let λ > 1. Let E₁,⋯,E_N ⊂ R^d be measurable sets such that

min |I ∩ Ej|∕|I| < 2−2dλ (1.1) 1≤j≤N

for any I. Then, there exist functions {f_j(x)}_j=1^N such that

N ∑ fj(x) ≡ 1, (1.2) j=1

0 ≦ fj(x) ≦ 1, 1 ≦ j ≦ N, (1.3)

fj(x) = 0 a.e. on Ej, 1 ≦ j ≦ N, (1.4)

∥fj|BMO ≦ c1(d,N )∕λ, 1 ≦ j ≦ N. (1.5)

Converely, if there exist {f_j(x)}_j=1^N that satisfy (1.2)–(1.4) and

∥fj|BMO ≦ c2(d,N )∕λ, 1 ≦ j ≦ N, (1.6)

then (1.1) holds.

Mathematical Subject Classification 2000

Primary: 42B10

Secondary: 46E99, 46J15

Milestones

Received: 20 April 1980

Published: 1 March 1982

Authors

Akihito Uchiyama

Vol. 99, No. 1, 1982

Akihito Uchiyama

Abstract

Mathematical Subject Classification 2000

Milestones

Authors