Strict local inclusion results between spaces of Fourier transforms

Walter Russell Bloom

Vol. 99 (1982), No. 2, 265–270

DOI: 10.2140/pjm.1982.99.265

Abstract

Let G denote a noncompact Hausdorff locally compact abelian group, Γ its character group, and write (L^s,l^t)^∧ for the space of Fourier transforms of functions in the amalgam (L^s,l^t). We show that for 1 ≦ p < q ≦∞ the local inclusion (L¹,l^p)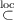^∧(L^∞,l^q)^∧ is strict, that is, given any nonvoid open subset Ω of Γ there exists f ∈ (L^∞,l^q) such that f −ĝ does not vanish on Ω for any g ∈ (L¹,l^p). If in addition G is assumed to be second countable then we show there exists such an f independent of the choice of Ω. Of special interest is the case, included in the above results, where the amalgams (L¹,l^q), (L^∞,l^p) are replaced by L^p(G), L^q(G) respectively.

Mathematical Subject Classification 2000

Primary: 43A25

Milestones

Received: 5 December 1979

Revised: 31 December 1980

Published: 1 April 1982