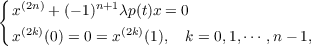Isoperimetric eigenvalue problem of even order differential equations

Sui Sun Cheng

Vol. 99 (1982), No. 2, 303–315

DOI: 10.2140/pjm.1982.99.303

Abstract

This paper is concerned with the following eigenvalue problem

(1)

where p(t) is assumed to be positive and continuous in [0,1]. For the class of functions q(t) which are equimeasurable to p(t), we shall show that the rearrangement of p(t) in symmetrically increasing order maximizes the least positive eigenvalue of (1), while the rearrangement of p(t) in symmetrically decreasing order minimizes it.

Mathematical Subject Classification

Primary: 34B25, 34B25

Secondary: 58F19

Milestones

Received: 7 May 1980

Revised: 13 October 1980

Published: 1 April 1982