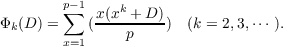Resolution of ambiguities in the evaluation of cubic and quartic Jacobsthal sums

Richard Howard Hudson and Kenneth S. Williams

Vol. 99 (1982), No. 2, 379–386

DOI: 10.2140/pjm.1982.99.379

Abstract

If p ≡ 1 (mod 2k) is a prime, the Jacobsthal sum Φ_k(D) is defined by

It is shown how to evaluate Φ₂(D) and Φ₃(D) for any integer D.

Mathematical Subject Classification

Primary: 10G15, 10G15

Milestones

Received: 15 February 1980

Revised: 27 October 1980

Published: 1 April 1982