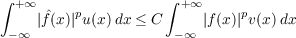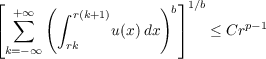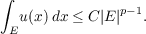On the search for weighted norm inequalities for the Fourier transform

Nestor Edgardo Aguilera and Eleonor Ofelia Harboure de Aguilera

Vol. 104 (1983), No. 1, 1–14

DOI: 10.2140/pjm.1983.104.1

Abstract

B. Muckenhoupt posed in [1] the problem of characterizing those non-negative functions u and v, which for some p, 1 ≤ p < ∞, the inequality

holds for any f, where f denotes the Fourier transform of f. In this paper we deal only with the case where either u ≡ 1 or v ≡ 1, finding that when v ≡ 1, 1 < p < 2, a necessary condition is that for any r > 0,

where b = 2∕(2 − p), and that a sufficient condition (v ≡ 1,1 ≤ p) is that for any measurable set E,

Similar conditions are obtained for the case u ≡ 1. Although we will show that the sufficient condition is not necessary (in §4, Corollary 1 and again in §6, Corollary 3 and Remark 4), we were unable to obtain any conclusions on our necessary condition.

Mathematical Subject Classification 2000

Primary: 42A38

Milestones

Received: 24 September 1980

Published: 1 January 1983