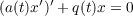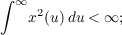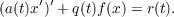|
Recently there has been an
interest in obtaining integrability criteria for solutions of nonlinear differential
equations similar in nature to those known for linear equations. In the classic
paper on the subject, H. Weyl classified the second order linear differential
equation
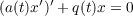 | (1) |
as being of the limit circle type if all its solutions are square integrable,i.e.,
otherwise the equation was said to be of the limit point type. In this paper we discuss
extensions of the limit point-limit circle classification to forced second order nonlinear
equations of the type
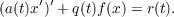 | (2) |
|