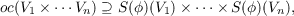Homomorphisms of minimal flows and generalizations of weak mixing

Douglas C. McMahon and Ta-Sun Wu

Vol. 104 (1983), No. 2, 401–416

DOI: 10.2140/pjm.1983.104.401

Abstract

In this paper we are concerned with generalizations of weakly mixing. Let ϕ : (X,T) → (Y,T) be a homomorphism of metric minimal flows and let S(ϕ) denote the relativized equicontinuous structure relation. The main result is that if ϕ has a RIM, λ, and z ∈ Z such that the support of λ_z equals the fiber X₀ = ϕ⁻¹(z), then:

and also there exists a dense set of points x₁,x₂,x₃,… in X₀ such that oc(x₁,x₂,x₃,…) ⊇ S(ϕ)(x₁) × S(ϕ)(x₂) ×… .

Mathematical Subject Classification 2000

Primary: 54H20

Milestones

Received: 9 April 1981

Published: 1 February 1983