|
|||||

|

|
|

|

|
|
On sums of
Rudin-Shapiro coefficients. II
John David Brillhart, Paul Erdős and Richard Patrick Morton |
|
Vol. 107 (1983), No. 1, 39–69
|
Abstract |
|
Let {a(n)} be the
Rudin-Shapiro sequence, and let s(n) = Σk=0na(k) and t(n) = Σk=0n(−1)ka(k). In
this paper we show that the sequences {s(n)∕ |
Mathematical Subject Classification 2000
Primary: 11N60
Secondary: 11N99
|
Milestones
Received: 13 January 1981
Published: 1 July 1983
|
Authors |
| John David Brillhart | |
| Paul Erdős | |
| Richard Patrick Morton | |
 |
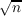
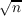

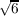
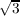
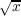 is shown to have a Fourier expansion whose
coefficients are related to the poles of the Dirichlet series
is shown to have a Fourier expansion whose
coefficients are related to the poles of the Dirichlet series  .
.