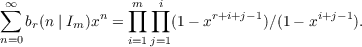A proof of the Bender-Knuth conjecture

Let b_r(n∣I_m) denote the number of r-rowed partitions of n whose parts lie in the set I_m = {1,2,…,m} and decrease strictly along each row. It is shown that

∑∞ m∏ ∏i br(n | Im )xn = (1− xr+i+j−1)∕(1 − xi+j−1). n=0 i=1 j=1

Mathematical Subject Classification 2000

Primary: 05A17

Secondary: 05A15

Milestones

Received: 30 October 1981

Published: 1 September 1983

Authors

Basil Gordon

Vol. 108, No. 1, 1983

Basil Gordon

Abstract

Mathematical Subject Classification 2000

Milestones

Authors