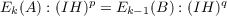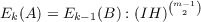The determinantal ideals of link modules. II

Lorenzo Traldi

Vol. 109 (1983), No. 1, 237–245

DOI: 10.2140/pjm.1983.109.237

Abstract

Let H be the multiplicative free abelian group of rank m ≥ 1. Suppose 0 → B → A → IH → 0 is a short exact sequence of ZH-modules, and the module A is finitely generated. Then B is also a finitely generated ZH-module, and for any k ∈ Z the determinantal ideals of A and B satisfy the equality

for all sufficiently large values of p and q. Furthermore, if this exact sequence is the link module sequence of a tame link of m components in S³, then

whenever k ≥ m.

Mathematical Subject Classification 2000

Primary: 57M25

Secondary: 13A15, 13E15

Milestones

Received: 27 January 1982

Published: 1 November 1983