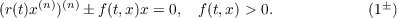Nonoscillatory solutions of (rxⁿ)ⁿ±f(t, x)x = 0

Allan L. Edelson and Jerry Dee Schuur

Vol. 109 (1983), No. 2, 313–325

DOI: 10.2140/pjm.1983.109.313

Abstract

We study the existence and growth rates of positive, monotonic, bounded solutions of the equations

First we prove our results for the linear equation with f(t,x) = p(t), then by a fixed point method we extend these to the nonlinear equation. We also obtain some oscillation results for (1^±).

Mathematical Subject Classification 2000

Primary: 34C10

Secondary: 34C11

Milestones

Received: 6 April 1981

Revised: 28 April 1982

Published: 1 December 1983