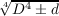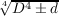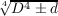On units of pure quartic number fields

Akira Endô

Vol. 109 (1983), No. 2, 327–333

DOI: 10.2140/pjm.1983.109.327

Abstract

Let K = Q() be a pure quartic number field, where D and d are natural numbers such that d divides D³ and d is fourth power free. Then 𝜀 = ±( + D)∕(−D) is a unit of K whose relative norm to the quadratic subfield of K is 1. We consider the condition for 𝜀 to be a member of a system of fundamental units of K.

Mathematical Subject Classification 2000

Primary: 11R27

Secondary: 11R16

Milestones

Received: 2 April 1981

Revised: 28 April 1982

Published: 1 December 1983