Hereditary cones, order ideals and half-norms

Derek W. Robinson and Sadayuki Yamamuro

Vol. 110 (1984), No. 2, 335–343

DOI: 10.2140/pjm.1984.110.335

Abstract

Let ℬ be an ordered normed space with positive cone ℬ₊ and let N be the canonical half-norm of ℬ₊, i.e.,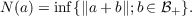

Then, for any hereditary subcone 𝒞 of ℬ₊, the positive bipolar 𝒞^⊥⊥ coincides with the N-closure 𝒞^N of 𝒞, i.e.,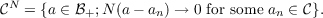

Similar facts are proved for order ideals and these results are used to derive a result of Størmer on archimedean order ideals.

Mathematical Subject Classification 2000

Primary: 46B30, 46B30

Secondary: 46A40

Milestones

Received: 13 May 1982

Published: 1 February 1984