The Jordan decomposition and half-norms

Derek W. Robinson and Sadayuki Yamamuro

Vol. 110 (1984), No. 2, 345–353

DOI: 10.2140/pjm.1984.110.345

Abstract

Let ℬ be a Banach space, with norm ∥⋅∥, ordered by a positive cone ℬ₊ and order the dual ℬ^∗ by the dual cone ℬ₊^∗. We prove that, if ℬ is orthogonally generated, each f ∈ℬ^∗ has an orthogonal, and norm-unique, Jordan decomposition f = f₊ − f₋ with f_±∈ℬ^∗,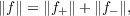

if, and only if, the norm on ℬ has the order theoretic property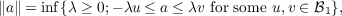

when ℬ₁ is the unit ball of ℬ. Various characterizations of the canonical half-norm associated with ℬ₊ are also given.

Mathematical Subject Classification 2000

Primary: 46B30, 46B30

Secondary: 46A40

Milestones

Received: 13 May 1982

Published: 1 February 1984