A Marcinkiewicz criterion for L^p-multipliers

Henry Dappa

Vol. 111 (1984), No. 1, 9–21

DOI: 10.2140/pjm.1984.111.9

Abstract

Suppose m is a bounded measurable function on the n-dimensional Euclidean space Rⁿ. Define a linear operator T_m by (T_mf)^ˆ= mf^ˆ , where f ∈ L² ∩ L^p(Rⁿ), 1 ≤ p ≤∞, and f^ˆ denotes the Fourier transform of f: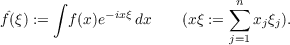

(We omit the domain of integration if it is the whole Rⁿ.) If T_m is bounded from L^p(Rⁿ) to L^p(Rⁿ), then m is called an L^p-(Fourier) multiplier, denoted m ∈ M_p(Rⁿ). The norm of m coincides with the operator norm of T_m.

Theorem 1. Let m and m′ be locally absolutely continuous on (0,∞) and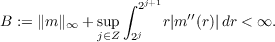

Then m(|ξ|) ∈ M_p(Rⁿ) for all p with 1 ≤ 2n∕(n + 3) < p < 2n∕(n − 3) ≤∞; in particular, ∥m∥_Mp(Rⁿ) ≤ cB with c independent of m.

Mathematical Subject Classification 2000

Primary: 42B15

Secondary: 42B25

Milestones

Received: 26 March 1981

Revised: 6 January 1982

Published: 1 March 1984