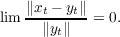|
In this paper we consider
the problem of the relative asymptotic equivalence of the solutions of the
systems
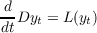 | (1) |
and
![-d[Dx − G(t,x )] = L(x )+ f(t,x ),
dt t t t t](a071x.png) | (2) |
where (1) is a linear system of neutral functional differential equations. The main
theorem gives conditions under which the following result is verified. Given a solution
yt of (1) there exists a solution xt of (2) such that
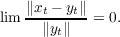 | (*) |
The converse of this result, namely given a solution xt of (2) there is a solution yt of
(1) such that (*) is satisfied is partially proved. A counterexample is given to show
that the converse result is not true in general.
|



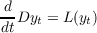
![-d[Dx − G(t,x )] = L(x )+ f(t,x ),
dt t t t t](a071x.png)