Inequalities for eigenvalues of the biharmonic operator

Gerald Norman Hile and R. Z. Yeh

Vol. 112 (1984), No. 1, 115–133

DOI: 10.2140/pjm.1984.112.115

Abstract

Let D be a bounded domain in R^m with smooth boundary. The first n + 1 eigenvalues for the problem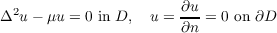

satisfy the inequality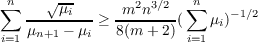

For the first two eigenvalues we have the stronger bound

μ2 ≤ 7.103μ1 (in R2),
μ2 ≤ 4.792μ1 (in R3).

The first two eigenvalues for the problem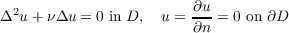

satisfy the inequality

ν2 ≤ 2.5 ν1 (in R2),
ν2 ≤ 2.12ν1 (in R3).

Mathematical Subject Classification 2000

Primary: 35P15

Milestones

Received: 13 April 1982

Published: 1 May 1984