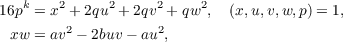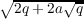|
For primes p = qf + 1,
Diophantine systems of the type
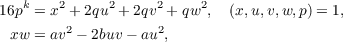 | (1) |
have been studied by Dickson, Whiteman, Lehmer, Hasse, Zee, and Muskat and Zee.
Virtually all these studies have centered on the special cases q = 5,13 (the
correspondence between the system (1) when q = 5 and the well-known system
introduced by Dickson is discussed in §3). For q = 13,29,37,53, and 61,
Hudson and Williams have proved that (1) has exactly eight solutions when
k = 1. For values of q ≡ 5 (mod 8) = a2 + b2 for which the class number
of the imaginary cyclic quartic field K = Q(i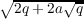 ) is greater than
one, (1) may or may not be solvable when k = 1. In §5 we examine families
of values of q and p for which there are eight solutions of (1) when k = 1
independent of any class number considerations. The existence of such families
is somewhat surprising, as is the fact that the question of solvability for
these families is independent of the primality of p or q (clearly we must
have q = a2 + b2) or the restriction p = qf + 1. Indeed the entire study
of systems of type (1) is restricted in the literature to primes p = qf + 1
artificially, as any completely general study should treat all primes p = qf + r,
(r∕q)4 = +1.
Hudson and Williams have proved that when the class number of K is not a
perfect square there are always solutions of (1) with p|(x2 −qw2). We call these zero
solutions and in this paper we examine the properties of such solutions in some detail
(see, particularly, §2).
A major contribution of our paper appears in §4 where we derive explicit
formulae for inductively generating all soutions of (1) for k > 1 given a basic
solution for k = 1. Finally in §7 we apply the formulae in §4 to illustrate the
Hudson-Williams-Buell extension of a theorem of Cauchy and Jacobi (see
[15]).
|
