On the KO-orientability of complex projective varieties

James M. Stormes

Vol. 114 (1984), No. 2, 469–480

DOI: 10.2140/pjm.1984.114.469

Abstract

The essence of the Riemann-Roch theorem as generalized by P. Baum, W. Fulton, and R. MacPherson is the construction of a natural transformation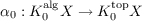

from the Grothendieck group K₀^algX of coherent algebraic sheaves on a complex quasi-projective variety X to the topological homology group K₀^topX complementary to the obvious natural transformation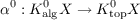

from the Grothendieck group K_alg⁰X of algebraic vector bundles on X to the Atiyah-Hirzebruch group K_top⁰X of topological vector bundles. Under this natural transformation, the class of the structure sheaf 𝒪_X corresponds to a homology class {X},

the K-orientation of X. Thus all varieties, singular or non-singular, are K-oriented, in contrast to the well-known fact that a smooth manifold M is K-orientable if and only if the Stiefel-Whitney class w₃M = 0 ∈ H³(M,Z).

Mathematical Subject Classification 2000

Primary: 55N15

Secondary: 14F05, 14F15

Milestones

Received: 15 October 1982

Published: 1 October 1984