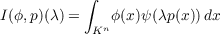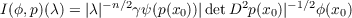|
For K a p-adic field, we
examine oscillatory integrals
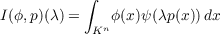
where ϕ is a Schwartz function on Kn, ψ is an additive character, λ ∈ Kx, and
p : Kn → K is locally analytic. If Dp≠0 on the support of ϕ, λ↦I(ϕ,p)(λ) has
bounded support. If Dp(x0) = 0 at exactly one point x0 in the support of ϕ but
D2p(x0) is non-degenerate, then
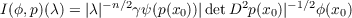
for sufficiently large |λ|, where γ is a complex eighth root of unity. An invariant
definition of wave front set, WFΛ(u), for distributions u relative to an open subgroup
Λ of K× is proved to exist, analogous to the classical case, with “rapidly decreasing”
replaced by “bounded support”. Definitions of pull backs and push forwards of
distributions, distribution products, and kernel maps are made, again similar to the
classical case, and their wave front sets computed. Wave front sets WFΛ(ρ) of
representations ρ of p-adic groups are also defined (cf. Howe, Automorphic forms,
representation theory, and arithmetic, Tata Inst., 1979, for the Lie group analogue).
For admissible representations ρ of, say, a semi-simple group G, with character χρ, we
show that WFΛ0(ρ) = WFΛ0(χρ), where WFΛ0(⋅) ⊆ Lie(G) is WFΛ(⋅) above the
identity element. Functorial properties of WFΛ(ρ) are developed and examples
computed.
|