An isoperimetric inequality for surfaces stationary with respect to an elliptic integrand and with at most three boundary components

Steven C. Pinault

Vol. 116 (1985), No. 2, 353–358

DOI: 10.2140/pjm.1985.116.353

Abstract

Let M be a connected C² two dimensional submanifold with boundary of R³, with at most three boundary components. Let Φ be a positive even elliptic parametric integrand of degree two on R³ ([5]), and suppose that M is stationary with respect to Φ. In this paper we show that there is a constant C(Φ) such that M satisfies the isoperimetric inequality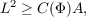

where L is the length of ∂M and A is the surface area of M. In the proof we also prove a lemma that M satisfies the inequality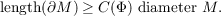

Mathematical Subject Classification 2000

Primary: 49F99, 49F99

Secondary: 53A05

Milestones

Received: 2 August 1983

Published: 1 February 1985