Vol. 117, No. 1, 1985
Recent Issues
Vol. 332: 1  2
Vol. 331: 1  2
Vol. 330: 1  2
Vol. 329: 1  2
Vol. 328: 1  2
Vol. 327: 1  2
Vol. 326: 1  2
Vol. 325: 1  2
Online Archive
Volume:
Issue:
     
The Journal
About the journal
Ethics and policies
Peer-review process
 
Submission guidelines
Submission form
Editorial board
Officers
 
Subscriptions
 
ISSN 1945-5844 (electronic)
ISSN 0030-8730 (print)
 
Special Issues
Author index
To appear
 
Other MSP journals
Some maximum properties for a family of singular hyperbolic operators

Zhu Jia Lu
Vol. 117 (1985), No. 1, 193–208
DOI: 10.2140/pjm.1985.117.193
Abstract

We study some maximum properties of solutions of the equation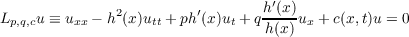

2 ′ h′(x)- Lp,q,cu ≡ uxx − h (x)utt + ph(x)ut + qh(x)ux + c(x,t)u = 0

with real parameters p and q. Some of the results here improve those of L. E. Payne and D. Sather. We also point out that a certain condition given by S. Agmon, L. Nirenberg and M. H. Protter is not only sufficient in order to obtain a kind of maximum property, but also necessary for a special case of Lp,q,c.
Mathematical Subject Classification 2000
Primary: 35B50
Secondary: 35L10
Milestones
Received: 9 May 1983
Published: 1 March 1985
Authors
Zhu Jia Lu