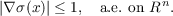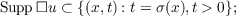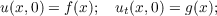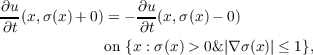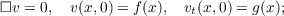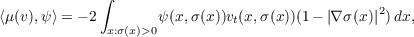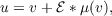|
We consider the following
problem: let x ∈ Rn, t ∈ R+, and let σ : Rn → R+ be a given lipschitz continuous
surface with lipschitz constant 1:
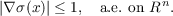 | (1) |
Let f ∈ Hloc1(Rn) and g ∈ Lloc2(Rn); then we prove that there exists a unique
solution of the following system of equations:
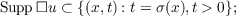 | (2) |
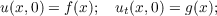 | (3) |
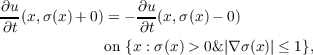 | (4) |
where □ = ∂2∕∂t2 − Δ is the wave operator in Rn × R+. The one-dimensional case
has been studied by M. Schatzman, who used it in the problem of a string compelled
to remain above an obstacle.
The difficulty in solving the problem lies in the fact that as σ2 may be
characteristic, one has to show that Equation (4) makes sense. More generally, we
show that, if u is a solution of finite energy of the wave equation, one may take traces
of ∂u∕∂t on either side of the non-characteristic parts of a non-time-like surface. We
make use of techniques from harmonic analysis, such as maximal functions on thin
sets, and Fourier integral operators.
Once this is done, we show that if v is the solution of the free wave equation
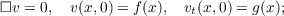 | (5) |
and if a measure μ(v) is defined on test functions by
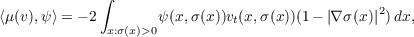 | (6) |
then the unique solution of Equations (2)–(4) is given by
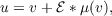 | (7) |
where ℰ is the elementary solution supported in t > |x| of the wave equation in
Rn × R+.
Our result represents a trend towards some kind of “hyperbolic capacity” theory;
it is known that one take traces of solutions of the Laplace and heat equations on sets
of elliptic (respectively, parabolic) positive Λ hyperbolic capacity. If one defines a
characteristic surface as a set of zero hyperbolic capacity, then we have proved that
one can take traces on subsets of positive hyperbolic capacity of time-like
surfaces.
|