|

|

|
|
On equivalences of
branched coverings and their action on homology
William H. Kazez |
|
Vol. 118 (1985), No. 1, 133–157
|
Abstract |
|
This paper studies equivalences of stable simple branched coverings of surfaces. We give necessary and sufficient conditions for a pair of homeomorphisms f and g of surfaces M and N respectively to be homologous to homeomorphisms and ḡ which form an equivalence of two prespecified stable simple branched covers ψ1 and ψ2. That is, homeomorphisms and ḡ such that 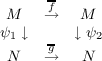 commutes are shown to exist if and only if ψ2∗f∗ = g∗ψ1∗ from H∗(M) to H∗(N). The proof relies on a uniqueness theorem of Hamilton and Berstein, Edmonds to restate the problem in terms of self equivalences of certain simple branched covers. Many equivalences of branched covers are constructed, and it is shown that the action on homology of these equivalences generates an appropriate subgroup of the symplectic group. |
Mathematical Subject Classification 2000
Primary: 57M12
|
Milestones
Received: 28 December 1983
Published: 1 May 1985
|
Authors |
| William H. Kazez | |
 |
