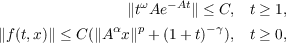Stability for semilinear parabolic equations with noninvertible linear operator

Milan Miklavčič

Vol. 118 (1985), No. 1, 199–214

DOI: 10.2140/pjm.1985.118.199

Abstract

Suppose that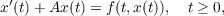

is a semilinear parabolic equation, e^−At is bounded and f satisfies the usual continuity condition. If for some 0 < ω ≤ 1, 0 < α < 1, αωp > 1, γ > 1,

whenever ∥A^αx∥ + ∥x∥ is small enough, then for small initial data there exist stable global solutions. Moreover, if the space is reflexive then their limit states exist. Some theorems that are useful for obtaining the above bounds and some examples are also presented.

Mathematical Subject Classification 2000

Primary: 34G20

Secondary: 35K22

Milestones

Received: 6 September 1983

Published: 1 May 1985